Kunci Jawaban
Kunci Jawaban Matematika Kelas 8 SMP Halaman 40 41 42: Tentukan Luas Segitiga Pada Gambar!
Pelajari kunci jawaban Matematika kelas 8 SMP halaman 40 41 42 Kurikulum 2013: Tentukan luas segitiga pada gambar!
Editor: Tim TribunNewsmaker
Pelajari kunci jawaban Matematika kelas 8 SMP halaman 40 41 42 Kurikulum 2013: Tentukan luas segitiga pada gambar!
TRIBUNNEWSMAKER.COM - Pelajari kunci jawaban Matematika kelas 8 SMP Semester 2 Halaman 40, 41, dan 42 Ayo Kita Berlatih 6.4. Kunci jawaban ini terdapat dalam Buku Matematika kelas 8 SMP Semester 2 Kurikulum 2013 untuk SMP/MTs, pada Bab 6: Teorema Pythagoras. Artikel ini akan menjelaskan kunci jawaban soal Ayo Kita Berlatih 6.4 yang ada di halaman 40, 41, dan 42. Kunci jawaban ini dapat digunakan oleh orang tua atau wali sebagai panduan untuk mengoreksi hasil belajar siswa.
Kunci Jawaban Matematika kelas 8 SMP Semester 2 Halaman 40 41 42 Kurikulum 2013
Ayo Kita Berlatih 6.4
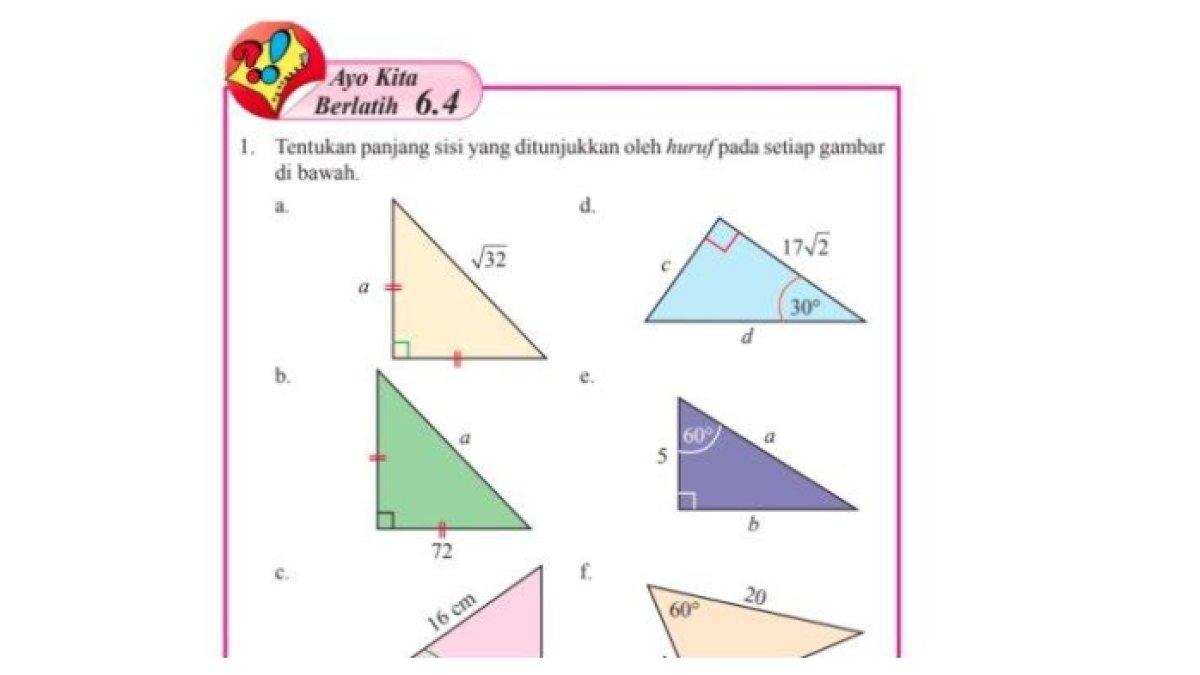
1. Tentukan panjang sisi yang ditunjukkan oleh huruf pada setiap gambar di bawah.
Kunci jawaban:
a) a⊃2; + a⊃2; = (√32)⊃2;
2a⊃2; = 32
a⊃2; = 32 / 2
a⊃2; = 16
a = √16
a = 4
Jadi, panjang sisi huruf a adalah 4.
b) 72⊃2; + 72⊃2; = a⊃2;
2 × 72⊃2; = a⊃2;
a = √(72⊃2; + 72⊃2;)
a = 72√2
Jadi panjang sisi huruf a adalah 72√2
c)b / 16 = √3 / 2
2b = 16√3
b = (16√3) / 2
b = 8√3
Jadi, panjang sisi huruf b adalah 8√3.
d) c / 17√2 = 1 / √3
√3 x c =17√2
c = (17√6) / 3
d / 17√2 = 2 / √3
√3 x d = 17√2 x 2
d = (34√6) / 3
Jadi, panjang sisi huruf c adalah (7√6) / 3 dan panjang sisi huruf d adalah (34√6) / 3.
e. a / 5 = 2/1
a = 5 x 2
a = 10
b / 5 = √3 / 1
b = 5 x √3
b = 5√3
Jadi, panjang sisi huruf a adalah 10 dan panjang sisi huruf b adalah 5√3.
f. d / 20 = 1/2
2d = 20
d = 20 / 2
d = 10
e / 20 = √3/2
2 x e = 20 x √3
e = (20√3)/2
e = 10√3
Jadi, panjang sisi huruf d adalah 10 dan panjang sisi huruf e adalah 10√3.
2. Tentukan keliling persegi ABCD
Kunci jawaban:
ABM membentuk Δ siku-siku sudut 90°, 45°, 45°
Sisi persegi (s) = AB = BC = CD = DA
Perbandingan AB : AC = 1 : √2
AB : 18√2 = 1 : √2
AB/18√2 = 1 : √2
AB = 18√2/√2
AB = 18
AB = BC = 18
Maka keliling = 4 x s
K = 4 x 18
K = 72
Jadi keliling persegi ABCD adalah 72
Baca juga: Tulislah Bentuk Pangkat yang Paling Sederhana, Jawaban Matematika Kelas 8 Hal 40 Kurikulum Merdeka
3. Tentukan luas segitiga pada gambar
Kunci jawaban:
alas = tinggi
A/C = 1/√2
a/16 = 1/√2
a = (1/√2) x 16
a = 8√2
L = ½ x 8√2 x 8√2
L = 64 cm⊃2;
Jadi luas segitiga pada gambar adalah 64 cm⊃2;
4. Apa yang salah dengan gambar di bawah ini? Jelaskan.
Kunci jawaban:
Segitiga siku-siku yang dimaksud bukanlah segitiga siku-siku dengan sudut 30°, 60°, dan 90°.
Karena perbandingan panjang ketiga sisinya tidak sama dengan 1 : 2 : √3.
5. Tentukan luas persegi panjang KLMN.
Kunci jawaban:
KLN membentuk Δ siku-siku sudut 90°, 30°, 60°
Diketahui: KN = A = lebar , KL = B = panjang, LN = C
A/C = 1/2
KN/8 = 1/2
KN = (1/2) x 8
KN = 4 KL/C = √3/2
KL/8 = √3/2
KL = (√3/2) x 8
KL = 4√3
L = panjang x lebar
L = 4√3 x 4
L = 16√3 cm⊃2;
Jadi luas persegi panjang KLMN adalah 16√3 cm⊃2;.
Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 41 Kurikulum Merdeka, Bab 1 Bilangan Berpangkat
6. Perhatikan gambar segitiga siku-siku ABC di bawah. Tentukan:
a. keliling segitiga ABC,
b. tentukan luas segitiga ABC.
Kunci jawaban:
Diketahui AD = 8 cm pada Δ ADC
Perhatikan Δ ADC siku-siku di D, ∠ CAD = 60° dan ∠ ACD = 30°
AC : AD = 2 : 1
AC : 8 = 2 : 1
AC = 8 × 2
AC = 16 cm
AD : CD = 1 : √3
8 : CD = 1 : √3
8 / CD = 1 / √3
CD = 8 × √3
CD = 8√3 cm
Perhatikan Δ BDC siku-siku di D, ∠ CBD = 30° dan ∠ DCB = 60°
Panjang BD
CD : BD = 1 : √3
8√3 : BD = 1 : √3
8√3 / BD = 1 / √3
BD = 8√3 × √3
BD = 8 × 3
BD = 24 cm
Panjang BC
CD : BC = 1 : 2
8√3 : BC = 1 : 2
8√3 / BC = 1 / 2
BC = 8√3 × 2
BC = 16√3 cm
a. Keliling segitiga ABC
Keliling Δ ABC = AD + BD + BC + AC
= 8 cm + 24 cm + 16√3 + 16 cm
= 48 cm + 16√3 cm
= 16 (3 + √3) cm
Jadi keliling segitiga ABC adalah 16 (3 + √3) cm
b. Menentukan luas segitiga ABC
Luas Δ ABC = 1/2 × AB × CD
= 1/2 × (8 + 24) cm × 8√3 cm
= 1/2 × 32 × 8√3 cm⊃2;
= 16 × 8√3 cm⊃2;
= 128√3 cm⊃2;
Jadi luas segitiga ABC adalah 128√3 cm⊃2;
7. Tentukan luas trapesium pada gambar.
Kunci jawaban:
30 derajat : 60 derajat : 90 derajat = 1 : √3 : 2
x =?
√3/2 = x/1
√3/2 = x
Mencari y
y =?
1/2 = y/1
1/2 = y
Mencari alas
√3/2 + √3/2 + 1
= √3 + 1
L = (jumlah sisi sejajar x t)/2
= ((1 + √3 + 1) x ½)/2
= ((√3 +2) x ½)/2
= (√3 + 2)/4
= 1/4√3 + 2/4
= 1/3√3 + 1/2
Jadi luasnya 1/3√3 + 1/2
8. Perhatikan gambar segitiga ABC di bawah ini. Diketahui ∠ABC = 90°, ∠CDB = 45°, ∠CAB = 30°, dan AD = 2 cm. Tentukan panjang BC.
Kunci jawaban:
Perbandingan sudut istimewa ΔBCD
∠CBD = 90°, ∠CDB = 45°, sehingga ∠BCD = 45°
CD : BC : BD = √2 : 1 : 1
BC = BD
Perbandingan sudut istimewa ΔABC
∠ABC = 90°, ∠CAB = 30°, sehingga ∠ACB = 60°
AC : BC : AB = 2 : 1 : √3
BC / AB = 1 / √3
BC / (AD + BD) = 1 / √3
BC / (2cm + BD) = 1 / √3
(√3)BC = 2cm + BD
(√3 - 1)BD = 2cm
BC = 2cm/(√3 - 1)
BC = 2cm/(√3 - 1) × (√3 + 1)/(√3 + 1)
BC = 2(√3 + 1)cm / (3 - 1)
BC = 2(√3 + 1)cm / 2
BC = (√3 + 1)cm
Jadi panjang BC adalah (√3 + 1)cm
9. Perhatikan balok ABCD.EFGH di samping. Jika besar ∠BCA = 60° , tentukan:
a. panjang AC,
b. luas bidang ACGE.
Kunci jawaban:
a. Perbandingan sudut istimewa ΔABC
∠BCA = 60°, ∠ABC = 90°, sehingga ∠BAC = 30°
AB : AC : BC = √3 : 2 : 1
AC : BC = 2 : 1
AC / 24dm = 2/1
AC = 48dm
b. BC = CG = 24dm
L ACGE = AC × CG
L ACGE = 48dm × 24dm
L ACGE = 1152dm⊃2;
10. Gambar di samping adalah jaringjaring piramida segitiga.
a. Berapakah panjang b?
b. Berapakah luas permukaan piramida?
Kunci jawaban:
a. Perbandingan sudut istimewa Δ siku-siku sama kaki
4cm : 4cm : b = 1 : 1 : √2
b : 4cm = √2 : 1
b = 4√2cm
b. Alas piramida adalah segitiga sama sisi yaitu b = 4√2cm, perbandingan sudut istimewa Δ setengah segitiga sama sisi.
4√2cm : 2√2cm : t = 2 : 1 : √3
t : 2√2cm = √3 : 1
t = 2√6cm
L piramida segitiga:
= L alas piramida + 3 L segitiga siku-siku
= (4√2cm × 2√6cm)/2 + 3 (4cm × 4cm)/2
= (8√3 + 24)cm⊃2;
Baca juga: Kunci Jawaban Matematika Kelas 8 SMP Halaman 30: Menentukan Persamaan Linear Dua Variabel
*) Disclaimer: Artikel ini hanya ditujukan kepada orangtua untuk memandu proses belajar anak.
Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.
(TribunNewsmaker.com/ Kufifah/ Tribunnews.com/ Muhammad Alvian Fakka)
| Kunci Jawaban Matematika Kelas 5 Halaman 61 Tentukan KPK dan FPB dari 45 dan 135 |

|
|---|
| Kunci Jawaban Bahasa Inggris Kelas 9 Halaman 59 What is Galang Wearing? |

|
|---|
| Kunci Jawaban Bahasa Inggris Kelas 9 Halaman 65 66 Bekantan is find/found in Kalimantan. |

|
|---|
| Kunci Jawaban Bahasa Indonesia Kelas 9 Halaman 46 "7 Langkah agar Membaca Selezat Mengudap" |

|
|---|
| Kunci Jawaban Bahasa Indonesia Kelas 4 Halaman 45 46 Bahas Bahasa |

|
|---|






