kunci jawaban
Soal & Kunci Jawaban Matematika SMA Kelas 10 Kurikulum Merdeka: Bab 8 Peluang dalam Nilai Mutlak
berikut ini adalah soal dan kunci jawaban matematika SMA kelas 10 kurikulum merdeka: bab 8 peluang dalam nilai mutlak
Editor: Tim TribunNewsmaker
TRIBUNNEWSMAKER.COM - Soal & Kunci Jawaban Matematika SMA Kelas 10 Kurikulum Merdeka: Bab 8 Peluang dalam Nilai Mutlak
Sebelum melihat kunci jawaban, ada baiknya siswa memahami materi matematika SMA kelas 10 Kurikulum Merdeka pada Bab 8 yang membahas mengenai peluang, dan mengerjakan latihan soal matematika bab 8 SMA kelas 10 Kurikulum Merdeka pada halaman 228-229 dengan baik dan teliti terlebih dahulu. Kunci jawaban hanya boleh dijadikan referensi jawaban siswa, berikut ini adalah soal dan kunci jawaban matematika kelas 10 Kurikulum Merdeka pada halaman 228-229:
Halaman 228 - 229
Latihan 8.3
Gunakan aturan penjumlahan untuk soal-soal berikut mengenai sepasang dadu yang dilempar.
1. Tentukan peluang mendapatkan dua angka sama atau berjumlah 5.
- Apakah kedua kejadian ini saling lepas atau tidak saling lepas?
- Peluang mendapatkan dua angka sama adalah P(A) = ?/36
- Peluang mendapatkan jumlah 5 adalah P(A) = ?/36
- Peluang mendapatkan dua angka sama dan berjumlah 5, P(A ∩ B) = …
- Maka peluang mendapatkan dua angka sama atau berjumlah 5 adalah …
Jawaban:
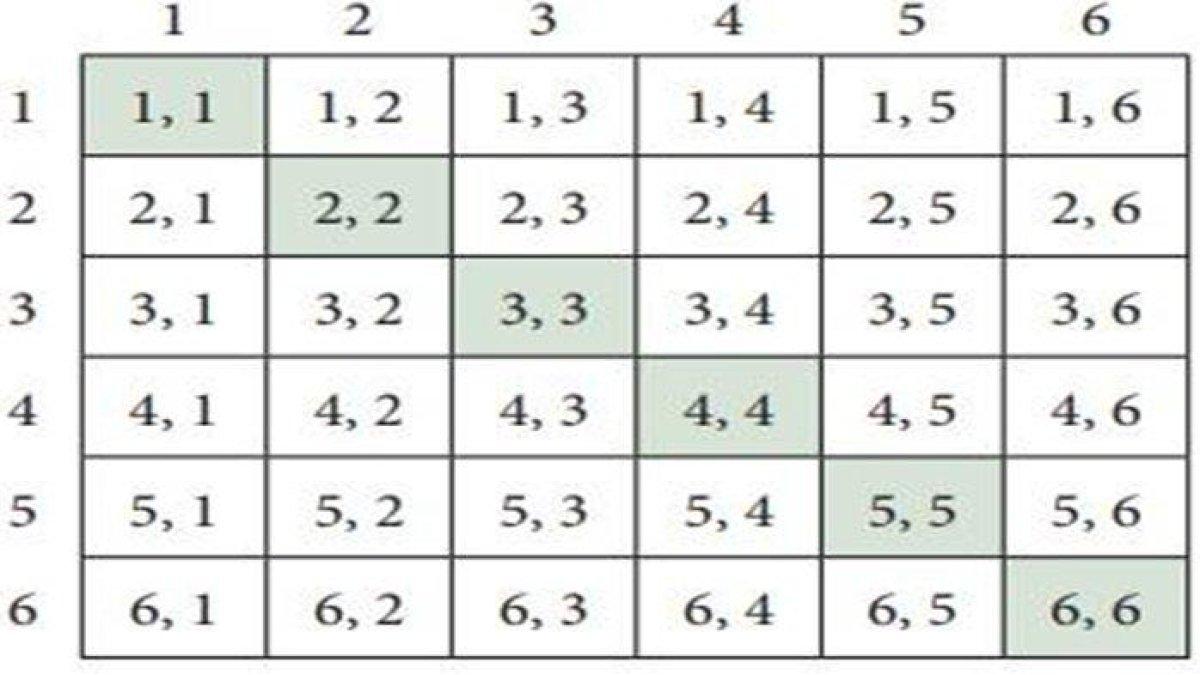
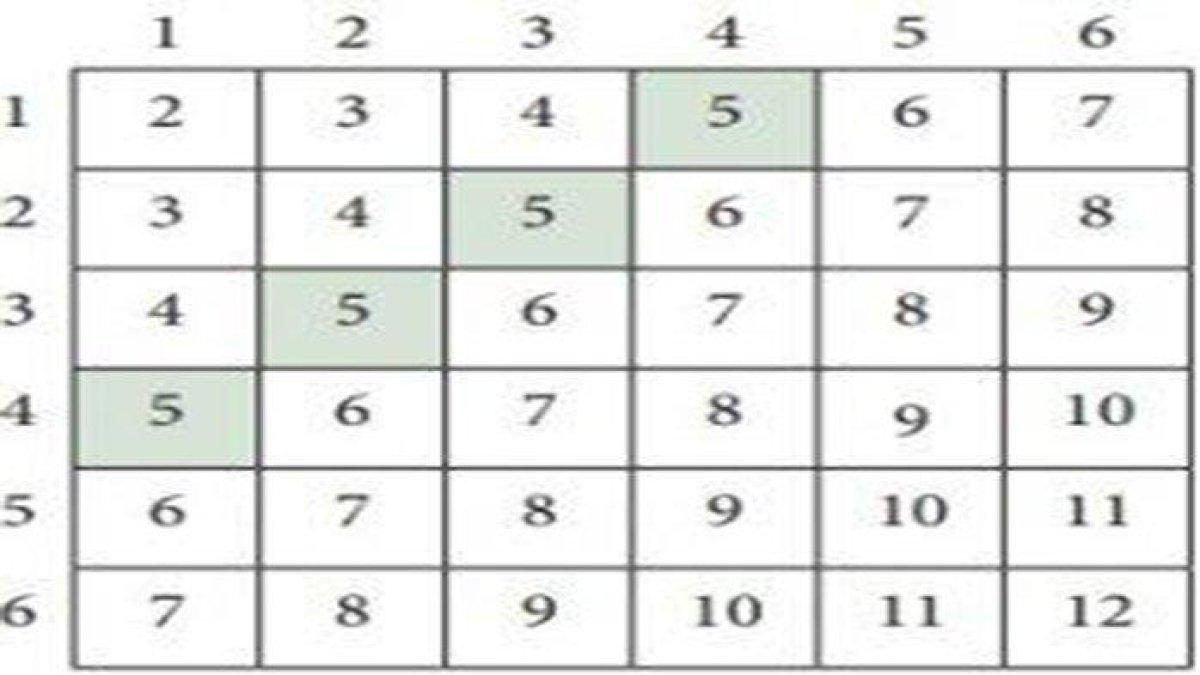
Peluang mendapatkan dua angka sama atau berjumlah 5. Dua kejadian ini saling lepas seperti dapat dilihat pada kedua tabel di atas yang menunjukkan hasil angka sama dan yang berjumlah 5.
Peluang mendapatkan angka sama adalah, P (A) = 6/36.
Peluang mendapatkan jumlah 5 adalah, P (B) = 4/36 .
Oleh karena itu, peluang mendapatkan angka yang sama atau berjumlah 5 adalah, P (A ∪ B) = P (A) + P (B) = 6/36 + 4/36 = 10/36
2. Tentukan peluang mendapatkan dua angka sama atau berjumlah 2.
- Apakah kedua kejadian ini saling lepas atau tidak saling lepas?
- Tentukan peluang mendapatkan dua angka sama, peluang mendapatkan jumlah 2, dan peluang mendapatkan dua angka yang sama dan berjumlah 2.
Jawaban:
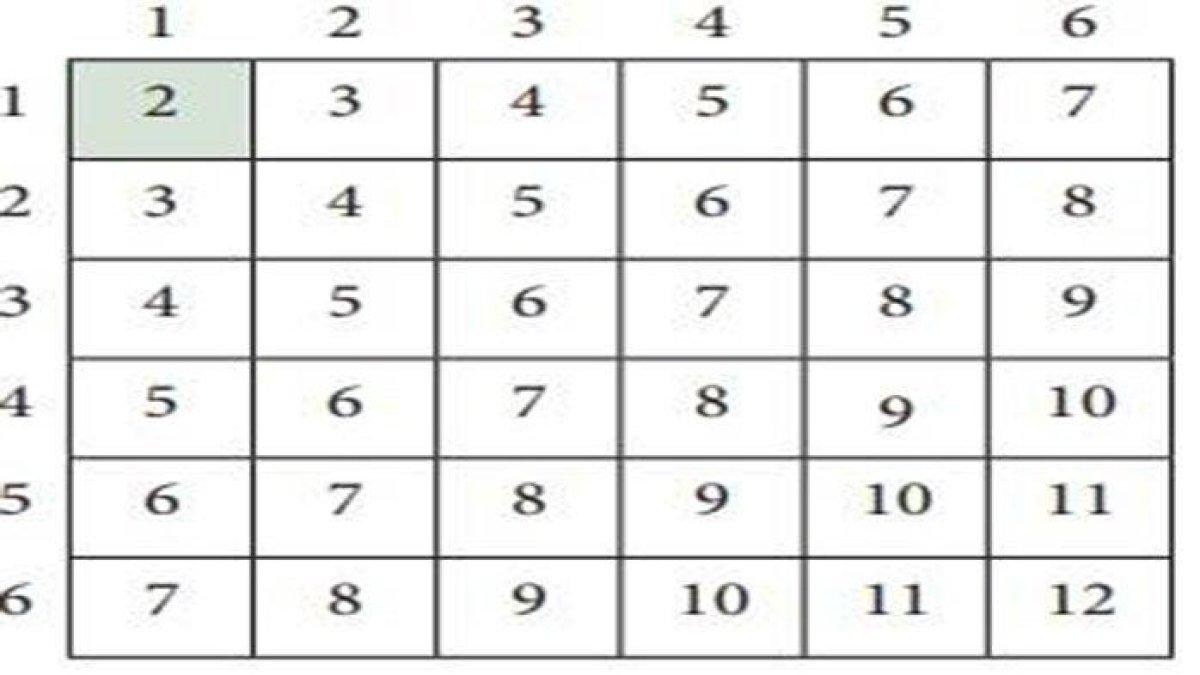
P (A) = 6/36
P (B) = 1/36
P (A ∩ B) = 1/36
Oleh karena itu, P (A ∪ B) = 6/36 + 1/36 - 1/36 = 6/36.
3. Tentukan peluang bahwa nilai mutlak dari selisihnya adalah 3 atau mendapatkan jumlah 5.
Jawaban:
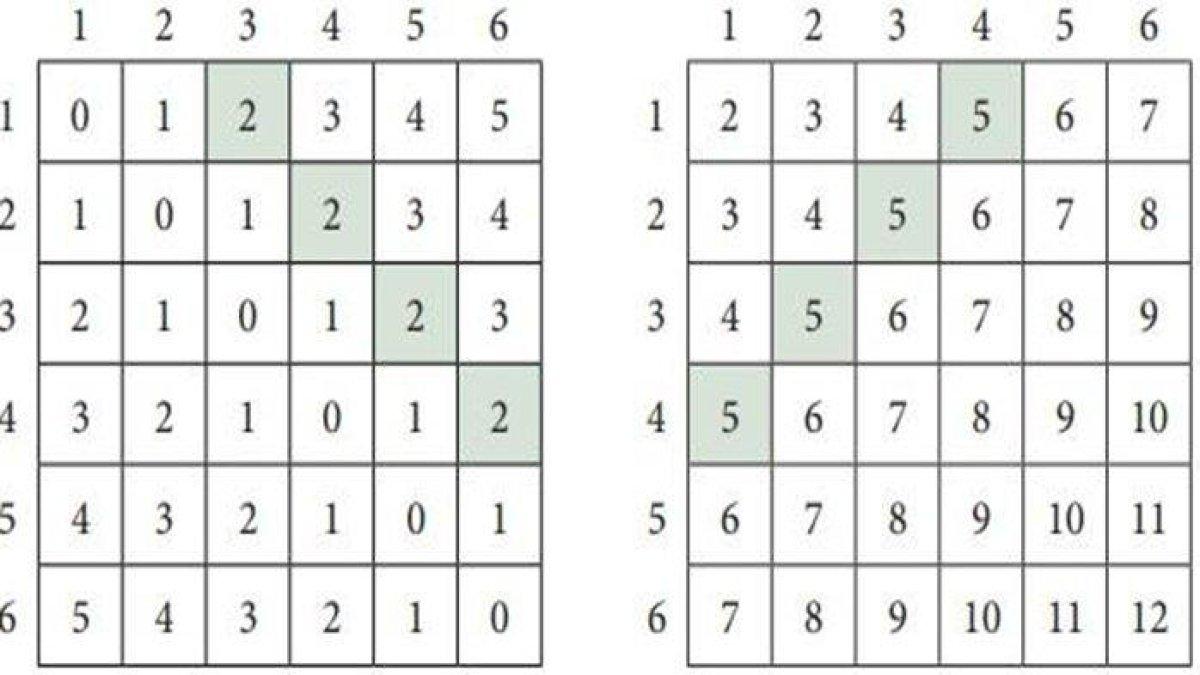
Kedua kejadian ini saling lepas seperti terlihat pada tabel ruang sampel di atas.
Kita juga bisa bernalar bahwa pasangan bilangan yang membentuk 5 adalah 1, 4 dan 2, 3, yang mana nilai mutlak dari selisihnya bukan 2, maka peluangnya adalah,
P (A ∪ B) = P (A) + P (B) = 8/36 + 4/36 = 12/36 = 1/3
4. Tentukan peluang bahwa nilai mutlak dari selisihnya adalah 2 atau mendapatkan jumlah 11.
Jawaban: Peluang bahwa nilai mutlak dari selisih adalah 2 atau mendapatkan jumlah 11 adalah, P (A ∪ B) = P (A) + P (B) = 8/36 + 2/36 = 10/36 = 5/18 karena
kedua kejadian adalah saling lepas.
*Artikel ini telah diolah sebelumnya di Tribunnews.com
| Kunci Jawaban Kalimat Definisi & Deskripsi Bahasa Indonesia Kelas 10 Halaman 17 Kurikulum Merdeka |

|
|---|
| Kunci Jawaban Ayo Berpikir Kreatif Geografi Kelas 12 Halaman 239: Dinamika Kerja Sama Antarnegara |

|
|---|
| Kunci Jawaban Activity D.1 Halaman 24 Bahasa Inggris Kelas 12: Isu Illegal Fishing di Laut Indonesia |

|
|---|
| Kunci Jawaban Grammar Focus Halaman 17 Bahasa Inggris Kelas 12: Memahami Mental Verbs |

|
|---|
| Kunci Jawaban Grammar Focus & Activity C.1 Bahasa Inggris Kelas 12 Halaman 18 Kurikulum Merdeka |

|
|---|






